수학 II 공식 - 유리함수(분수함수)와 점근선의 교점의 최소 거리

 

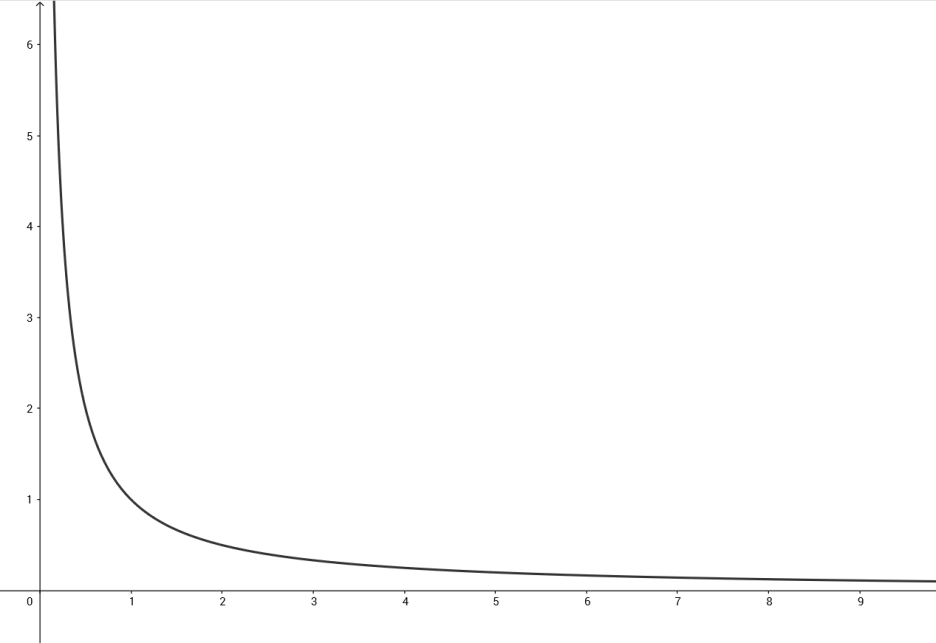
※유리함수의 그래프

- y=1/x

수학 II의 "유리함수와 무리함수" 단원에서, 우리는 새로운 유리함수의 형태인 분수함수를 배우게 되는데요, 한 단원의 제목을 차지하고 있는 만큼 수학 II를 공부할 때 당연히 비중 있게 공부해야 하는 함수입니다.

 

위의 그림은 가장 대표적인 분수함수인 "y=1/x"의 그래프입니다.

이 그래프에는 여러 가지 특징들이 있습니다. 원점에 대해 점대칭이며, 원점을 지나는 직선 "y=x", "y=-x"에 대해서 선대칭되어 있습니다. 역시 가장 큰 특징으로는, 분수함수는 공통적으로 점근선을 가진다는 것입니다.

 

※점근선

점근선의 정의를 글로 쓰면, "곡선 위의 한 점이 어떤 직선에한없이 가까이 근접할 때의 그 직선"이라고 합니다. "y=1/x"라는 그래프의 점근선은 x축, y축이죠. 점근선을 가지는 것은 분수함수의 가장 중요한 특징 중 하나이기 때문에, 이 두 점근선을 가지고 문제를 내는 경우가 많습니다.

- x축과 y축을 향해 한없이 근접한다.

※공식

 

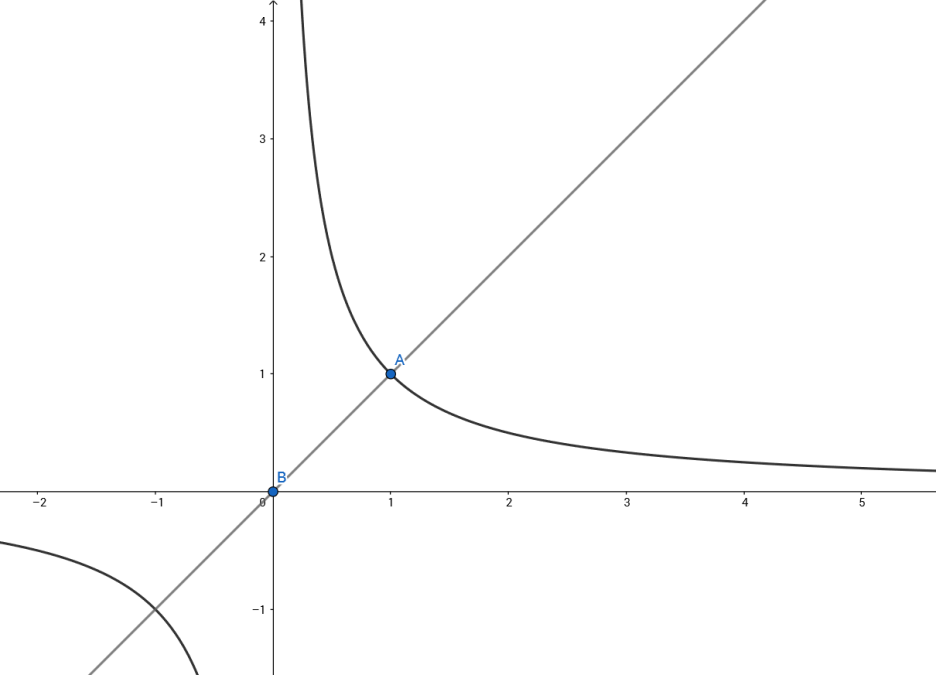
오늘 다룰 공식은 "분수함수와 점근선의 교점의 최소 거리"입니다.

즉, 그림에서 선분 AB의 길이를 구하는 목적의 공식입니다.

 

물론 저 길이를 구하는 것 자체는 어려운 일이 아닙니다.

식을 세우고 교점을 구해 보면 어떤 분수함수도 오래 걸리지 않고 답을 낼 수 있습니다.

그러나 공식의 목적은 "오래 걸리지 않는" 것이 아니라, "즉각적으로" 답을 내도록 하는 것입니다. 또한 공식을 보시면 알겠지만, 놀라울 정도로 짧고 간결해서 직접 계산하는 일보다는 훨씬 문제 풀이 속도를 수월하게 해 줍니다.

 

그래서 일반화된 함수에서 문제를 풀어보았습니다.

이 문제의 풀이에는 기울기가 1이면서 (p, q)를 지나는 직선의 식을 세워서 풀 수도 있지만, 수학적으로 명확한 풀이가 아니기 때문에 저는 산술-기하평균을 이용한 풀이를 적어보겠습니다.

 

결론적으로,

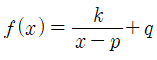
라는 분수함수에서, "분수함수와 점근선의 교점의 최소 거리" 는

입니다.

이 공식이 매력적인 것은 k값 하나만 알면 거리를 바로 알 수 있다는 것입니다. 저도 공식을 유도하기 전에는 깨닫지 못했었지만, 만들어진 공식을 보니 k값에 따라 개형이 결정되므로 k값만 알면 거리를 알 수 있다는 사실이 직관적으로 보입니다.

어렵지 않은 증명이니 수학을 좋아하시는 분은 한 번 스스로 해보셔도 좋을 것 같습니다. 특히 수학(하)를 이제 학습해야 하는 예비 고1이라면 학교 시험에서 문제를 빠르게 푸는 데도 도움이 될 것이라고 생각합니다.

 

※예제

마지막으로 간단한 예제를 하나 소개하고 글을 마치겠습니다.

위의 공식을 잘 활용하면 충분히 암산할 수 있을 겁니다! 따라서 굳이 풀이를 적지는 않겠습니다.